2.1.2. BINARY number system

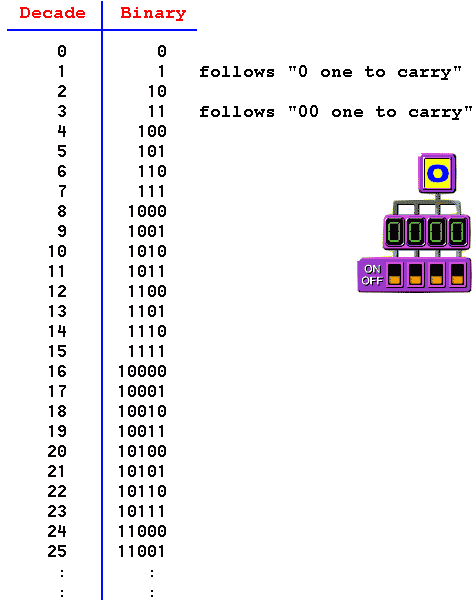
In decade numbering system, the number 'zero, one, two, three, four, five, six, seven, eight, nine, TEN, and 'ten' is essentially 'zero one away'. For the binary number system used names two digits of decade system; zeros (0) and one (1). Counting in binary number system starts with the description 'zero, one, zero one away'. At each new derived binary number is added to the value "1". Analogous to the above one can build a binary number system of the example in Table 2.1.1.

Table* 2.1.1 Generate a series of binary integers.

According animation from the previous picture, it is clear that the binary system of numbers discern only two states: 'on' or 'off'. Performance electronics that will monitor only the two conditions and their changes is much easier to make than to simultaneously monitor ten different states, analogous performance switches with two positions (as shown) and the ten-position switch. It is not surprising that the work of a digital computer is based precisely on the binary number system.

The general form for the conversion of a binary number in the decade number is:

Example I

What is the decade value of the binary number 10101101B, according to the sign of the ' I ' in Figure 1.1.3.

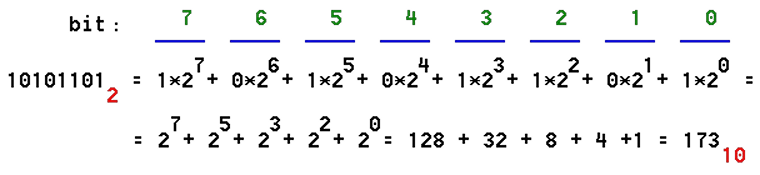Zero bit, first from right, carries a minimum weighting value (least significant bit), and their weights increasing from right to left. The leading bit, first from the left, has the highest weighting value (bit of greatest importance).

Thus, the conversion of binary numbers in the decade's very simple.

For binary numbers less than one process is analogous to the actions the decade numbers e.g. 0.101B number is:

0.101₂ = 1•2^-1 + 0•2^-2 + 1•2^-3 = 1/2 + 1/9 = 0.61111...₁₀

Example II

What is the binary value of the decade number 47?

Dividing the decade number by two and forming a series of integer residue is obtained decade equivalent of the binary number by amount.

Example III

For numbers less than one conversion is done by multiplying the two and forming a series of redundant integer calculation example the decade number 0.8215.

Should take account of the pronunciation of binary numbers. One can not say for 101111B 'Hundred and one thousands, and one hundred and eleven', as an excuse implies decade contents, but it should say 'one, zero, one, one, one, one based on two'.

Example IV

How many binary digits ' a ' should be used to display a set of natural numbers (positive integers) of 0-N?

The number of binary combinations should be equal to or greater than the decimal number N, and valid relation is:

2^a >= N   , from which comes:

a >= log₂ ( N )   , or shorter:

a >= ld ( N )

The required number of binary digits is the first integer greater than the calculated result. Calculating the logarithm of the base ' 2 ' today with modern calculators is not an issue of importance.

The binary number system is the basis upon which a computer to perform their tasks in the control level. Presentation of numerical results in binary format is very vast and incomprehensible to the user of a multitude of digits, and as an intermediate stage to decade system of numbers used by octal and hex number system. As usual computer user, and very rarely, and professional in the IT field, as a rule, do not directly use the binary number system, a description of the binary number system on this web site is entirely sufficient to further understand the elements that describe the principles on which a computer system works.

2.1.3 OCTAL number system

In addition to the binary number system used in computers and OCTAL number system with base 8 and who uses the names and signs (graphemes) of decade numbering system and the digits 0,1,2,3,4,5,6 and 7, numbers of this system are shown in the following table:

Table 2.1.2 Generating a decade and octal series of integers.

The general form of the conversion octal number in the decade is:

Example V

What is the decade value of the octal number 423o?

423₈= 4•8² + 2•8¹ + 3•8⁰ = 256 + 16 + 3 = 275₁₀

Since 7 is a binary digit combination 111B, dividing the binary number into groups of three digits, it is easily converted to the octal number:

How is one to represent the characters (graphemes) used mostly 8-bit binary combinations, this number system was its use in the very beginning of the design of a digital computer when the one character used 7 bits. However, expansion into different markets was only possible with some modifications for local graphemes, which led to the application of 8-bit words to describe the combination of characters. Almost the entire present-day software in the event display binary content is designed to show groups of 4 bits, and two groups for each character to ASCII code, generally accepted recommendations for coding graphemes, and is therefore more practical hexadecimal number system in which for each sign used by two hexadecimal digits. To monitor developments in the computer, or define some parameters such as color code in GIF format images or background colors web-site, rather it uses hex representation of the binary, because the number of binary digits in the number of large and as such is unclear.