2.1.4. HEXADECIMAL number system |
In the hexadecimal number system is a base 16 system, and the addition of known shape and called digits 0,1,2,3,4,5,6,7,8 and 9 for the remaining digits of graphemes using the letters A, B, C, D , E and F as in numbers greater than 9 should use two characters. Of course, they were able to invent a new graphic shapes (graphemes) for displaying the 16 hexadecimal digits or just for an extra six digits, and for them a new name, but it is a problem with no particular significance.
Thus, the hexadecimal digits of from 0 to F hexadecimal by labeling or 0-15 per decade understanding of their value. Numbers hexadecimal system are shown in the following table:
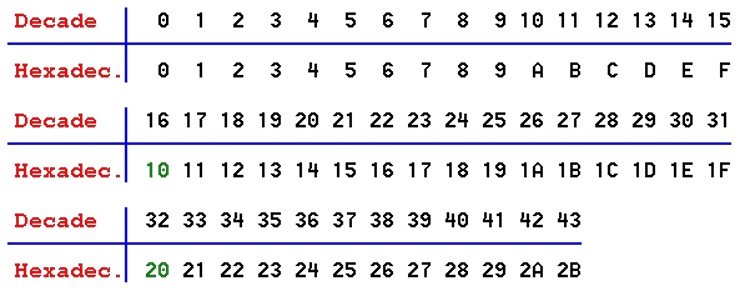 |
| Table 2.1.3 Generating decade and hexadecimal series of integers. |
The general form for converting a hexadecimal number in the decade is:
 |
Dividing the binary number into groups of 4 digits in a group, it can be very easily made his conversion to hexadecimal, as in the analysis of Table 2.1.1 recognized that each hexadecimal digit display with 4 bits.
 |
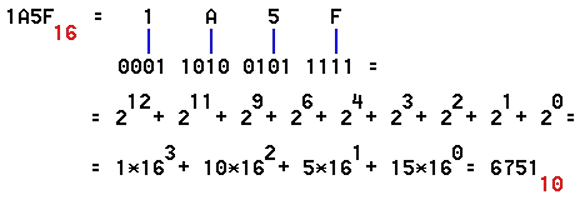
First group up to the "0" in order to fill and was credible in the view (the leading zero), which is mathematically correct. Convert hexadecimal number to binary is done reverse procedure:
 |
Sixteen-bit binary number can use the hexadecimal numbering system very appropriate show. Conversion is quite simple and provides rapid understanding of the contents Readings in computer memory or in its second part. That is why the need of knowing the displayed numeric system.
Convert from octal in hexadecimal system and vice versa is simple, the number is converted into binary and then grouped into groups of four or three digits and converted to another form.
61548 = 110 001 101 1002 = 1100 0110 11002 = C6C16 = 318010
Direct conversion decade number in octal is possible according to the same principle as the conversion to binary. But the simplest is the decade number converted to binary and then binary grouping of binary digits into a hexadecimal or octal, as appropriate.
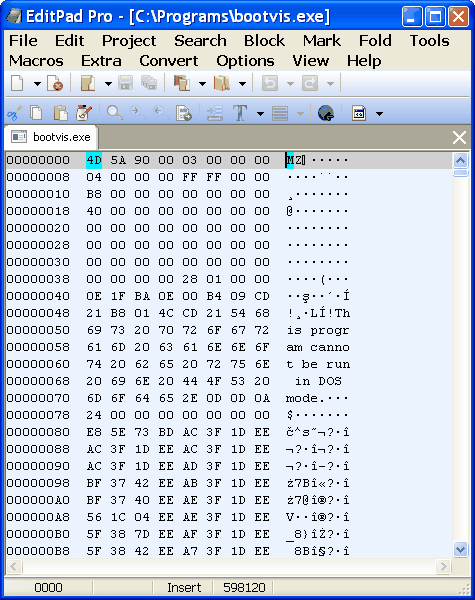
However, for reasons of clarity during the activities of system the results are present to user mostly into decimal number system. To view content of files using the dedicated editors that the user can visualize the contents of any file in ASCII, hex code or in both codes at the same time as shown in the following image.
 |
|
| Figure 2.1.4 Overview and editing of file. |
The figure shows that the examination of the hex file contents, print displayed in columns of eight heksadekadnih digits in the column, and according to the example at Figure 2.1.4 window of file editor is narrow so that it can display only one column. Better educated users in this file editor recognizes a lot more data; header of file, addresses for calling program routines within the file or from some other library file, it can change some conditions of program execution and the like. Thus, the basic tool of 'hackers'. In addition, the Windows operating system used in its database system (registry) records in hexadecimal format, and in this respect the knowledge of the number system has significant justification. An example of use of the hexadecimal editor is shown in Figure 4.6.37.
Basic and smallest element in a combination of pulses is the chance of a place in the combined pulse reaches the positive or negative impulse, or "0" or "1". The choice between "0" and "1" represents the lowest possible choice and represents a measure of the amount of information called BIT (BInary digiT). By ASCII set of 8 b (eight bits) represents a single character. According to the agreement the combination is called a BYTE (BinarY TErm).
So:
8 b (bit) = 1 B (Byte)
Larger units to measure the amount of information of the above are:
1 kB (kilo Byte) = 1'024 B
1 MB (Mega Byte) = 1'024 kB = 1024 • 1024 B =
= 1'048'576 B
1 GB (Giga Byte) = 1'024 MB = 1024 • 1024 kB =
= 1024 • 1024 • 1024 B =
= 1'073'741'824 B
1 TB (Tera Byte) = 1'024 GB = 1'048'576 MB =
= 1'073'741'824 kB =
= 1'099'511'627'776 B
If we take account of an agreement that one byte is eight bits, their relationships should be counted as follows:
1 kb (kilo Bit) ) 1'024 b
1 Mb (Mega Bit) = 1'024 kb = 1024 • 1024 b =
= 1'048'576 b
1 kB (kilo Byte) = 1024 • 8 b = 8'192 b
1 MB (Mega Byte) = 1024 • 8 kb = 1024 • 1024 • 8 b =
= 8'388'608 b
If it is said that the media has a memory CAPACITY of 4 MB, in simple terms it means that it is possible to save 4'194'304 B, or characters, in the size of 8 b (eight bits) each.
Multiplier of 1024 is the result of a mathematical expression:

|
|
and that is the decade amount of binary number: 10'000'000'000 B (ten zeros).
As computer (digital) uses only numbers, it means that all characters, instructions and data must be converted to numbers to be understood by the computer. Signs and instructions are usually entered via a computer keyboard that sends the appropriate combinations of pulses. Generally, the keyboard is an electromechanical converter that sign on the keys by pressuring her into a corresponding binary combination of him. Each character belongs to him inherent binary combinations. Character sets and binary combination is called a CODE, and the creating of binary combination is called ENCODING.
From recent human history, the joining of pulses, electrical or lighting, or similar, individual characters letter is known as the 'Morse alphabet'. The computer uses the same principles in the more advanced form.
From the above it is clear that computers can not successfully exchange data with each other if you do not use the same code, and is of great importance to the standardization of code and his respect, and his knowledge.
Since the letter ' k ' (kilo) under the international metric system, the SI system of units, then 1000 (one thousand), according to a contradiction with the generally accepted system of measurement units. Therefore, by the IEC (International Electrotechnical Commission) 1998. The binary size of the proposed units kibi, mebi, gibi ..., as shown in the following table.
|
Prefixes and the decade of the size of the binary |
||||
| Factor | Name | Symbol | Decade value | Comparison with SI |
| 210 | kibi | Ki | kilobinary: (210)1 | kilo: (103)1 |
| 220 | mebi | Mi | megabinary: (210)2 | mega: (103)2 |
| 230 | gibi | Gi | gigabinary: (210)3 | giga: (103)3 |
| 240 | tebi | Ti | terabinary: (210)4 | tera: (103)4 |
| 250 | pebi | Pi | petabinary: (210)5 | peta: (103)5 |
| 260 | exbi | Ei | exabinary: (210)6 | exa: (103)6 |
|
| ||||
|
Comparison of binary size with similar examples by SI standard | ||||
| one kibibit | 1 Kib = 210 bit-a = 1024 b | |||
| one kilobit | 1 kb = 103 bit-a = 1000 b | |||
| one kibibyte | 1 KiB = 210 Byte-a = 1024 B | |||
| one kilobyte | 1 kB = 103 Byte-a = 1000 B | |||
| one mebibyte | 1 MiB = 220 Byte-a = 1 048 576 B | |||
| one megabyte | 1 MB = 106 Byte-a = 1 000 000 B | |||
| one gibibyte | 1 GiB = 230 Byte-a = 1 073 741 824 B | |||
| one gigabyte | 1 GB = 109 Byte-a = 1 000 000 000 B | |||
| one tebibyte | 1 TiB = 240 Byte-a = 1 099 511 627 776 B | |||
| one terabyte | 1 TB = 1012 Byte-a = 1 000 000 000 000 B | |||
| one pebibyte | 1 PiB = 250 Byte-a = 1 125 899 906 842 624 B | |||
| one petabyte | 1 PB = 1015 Byte-a = 1 000 000 000 000 000 B | |||
| one exbibyte | 1 EiB = 260 Byte-a = 1 152 921 504 606 846 976 B | |||
| one exabyte | 1 EB = 1018 Byte-a = 1 000 000 000 000 000 000 B | |||
|
|
||||
It is important to note that the proposed prefixes for binary multiples are not part of the International System of Units (SI) - the metric system. But for ease of understanding prefixes are derived from the SI prefix as positive powers of ten. The name of each binary prefix derived from the name of the corresponding SI prefix by retaining the first two letters of the SI prefixes and adding the letters ' bi ', which recalls the word 'binary'. Similarly, the symbol of each new prefix binary symbols derived from the corresponding SI prefix by adding the letter ' i ', which again recalls the word 'binary'. Stated somewhat shyly enters into practice.
By the way, capital letter ' K ' (Kelvin) stands for temperature according to the SI system.
SUMMARY:
Application binary number system in computer technology is justified because of the two benefits that the system provides:
- Reliability
- Economical
Reliability can be easily and safely achieved because the electronic circuit needs to take only two states: there is no voltage, or "1" or "0", simply 'working' or 'not working'. If, in addition to each binary combination will add a number in a way that each ensure the total number of units or even zero (the parity check), or a numerical total is calculated as the total sum of all numbers within a certain 'block' of data - control sum (check sum) that are associated with him, block transfers, and similar to the above, contributes to the overall reliability of the system and control the occurrence of errors. Economy is reflected in the need for a minimum number of lines for the transmission of signals over a distance.
Regarding the conversion of numbers from one system to another can be used in Windows operating systems software called 'Calculator' - enabled /View/-/ Scientific/, scientific calculator as a device of some of the companies that produce them, or simple 'JavaScript' calculator at site 'https://www.periodni.com/'.
|
Citing of this page: Radic, Drago. " Informatics Alphabet " Split-Croatia. {Date of access}; https://informatics.buzdo.com/file. Copyright © by Drago Radic. All rights reserved. | Disclaimer |